Introduction

Qu’est-ce que le Megabot ?

Le Megabot est un robot quadrupède de grande envergure pouvant transporter un passager et dont la vocation première est d’être présenté lors d’évènements liés à la robotique. Il pèse plus ou moins 250 kg, mesure environ 2,50 m de largeur et est actionné via des vérins électriques. Sa conception ainsi que sa construction ont été réalisées par Julien Allali , maître de conférence à l’ENSEIRB-MATMECA, et il est actuellement conservé au Fablab de Bordeaux INP.

Mission

L’objectif de ce projet est dans un premier temps de revoir le contrôle du robot en améliorant son modèle cinématique, c’est à dire revoir l’ensemble des algorithmes effectuant la traduction d’un ordre de position en une commande d’élongation de vérins. Après cela, il s’agit d’implémenter un algorithme de marche afin que le robot puisse suivre un déplacement courbe. Enfin, afin de vérifier la validité des algorithmes implémentés indépendemment des contraintes réelles telles que la déformation de la structure sous son poids, il faudra modéliser le Megabot et l’intégrer au simulateur PyBullet.  

Contrôle

Le contrôle a pour objectif l’établissement de la cinématique inverse du Megabot, c’est à dire l’implémentation d’un ensemble de méthodes permettant de déterminer les élongations des 12 vérins nécessaires à l’obtention d’une position donnée. En général la cinématique inverse peut être calculée par des bibliothèques dédiées en leur fournissant un modèle URDF du robot (par exemple pinocchio en python). Néanmmoins, cette option n’a pas pu être mise en place dans le cas du Megabot pour 2 raisons :

• Le format URDF construit un arbre dont les sommets sont les différentes pièces du robot et dont les arcs sont les liaisons entre ces pièces (glissière, pivot, etc). La structure du Megabot incorporant des fermetures géométriques, cela impliquait la formation de cycles au sein de l’arbre, ce qui est impossible.

• Dans l’hypothèse ou nous modélisions le Megabot par un arbre en supprimant ses fermetures géométriques et en simulant un robot actionné par des moteurs aux articulations, nous aurions alors une minimisation de l’erreur dans notre cinématique inverse qui porterait sur les angles de nos articulations et non sur nos élongations de vérins.

Nous avons donc décidé de redéfinir clairement la cinématique du Megabot.

Cinématique du Megabot

Etablir le modèle cinématique direct d’un robot consiste à élaborer un ensemble de méthodes de calcul permettant de déterminer la position du robot à partir de valeurs articulaires d’entrée. Dans notre cas, il s’agit de créer une ou un ensemble de fonctions prenant en entrée des élongations de vérin valides et retournant la position du Megabot. Ce problème est solvable de manière analytique assez simplement.

Etablir le modèle cinématique inverse d’un robot en revanche consiste à faire le travail inverse : on veut obtenir les valeurs articulaires à partir d’une position d’entrée. Ce sens est bien plus complexe que le précédent et ne peut pas être résolu de manière analytique dans bien des cas, dont celui du Megabot.

Une solution classique à ce problème est d’avoir recours à la matrice jacobienne associée au modèle cinématique direct : il s’agit de la matrice des dérivées partielles de notre cinématique directe. En effet, elle permet d’approximer linéairement dans le cas de petites variations la relation entre nos valeurs articulaires et nos valeurs de position dans le sens direct. Une fois cette jacobienne \(J\) déterminée, il devient possible de déterminer le modèle cinématique inverse en résolvant un problème d’optimisation quadratique de la forme :

Ce problème, où \(\Delta V\) est le vecteur des variations des élongations des vérins à déterminer, \(J\) la jacobienne de la cinématique directe et \(\Delta X\) le vecteur des variations de position, minimise effectivement l’erreur quadratique sur \(\Delta X\) tout en permettant de contraindre \(\Delta V\) avec les variables \(G\), \(h\), \(A\), \(b\), \(lb\) et \(ub\). Ces variables de contraintes sont utiles pour contraindre les élongations de vérins à ses limites physiques par exemple.

Intro test

Détails de la démonstration

Cette façon de résoudre la cinématique inverse est un exemple d’application de la méthode des moindres carrés. La résolution de ce problème quadratique est réalisable à l’aide d’un solveur QP tel que \(\verb|qpsolvers|\) en Pyhton.

Calcul de la jacobienne de la cinématique directe

Nous allons a présent élaborer la matrice jacobienne associée à la cinématique directe du Megabot. Nous l’élaborerons tout d’abord relativement à une patte dans son plan avant de la généraliser à l’ensemble des pattes dans le référentiel monde.

Cinématique directe dans le plan de la patte

Pour déterminer la jacobienne associée à notre cinématique directe dans le plan de la patte, il est nécessaire de formaliser notre problème. Nous allons calculer successivement les écarts de position des points \(D\), \(E\), \(F\), \(G\), \(H\), \(I\) et \(J\) représentés sur le schéma suivant en fonction des variations d’élongation \(\Delta v_1\) et \(\Delta v_2\) des vérins.

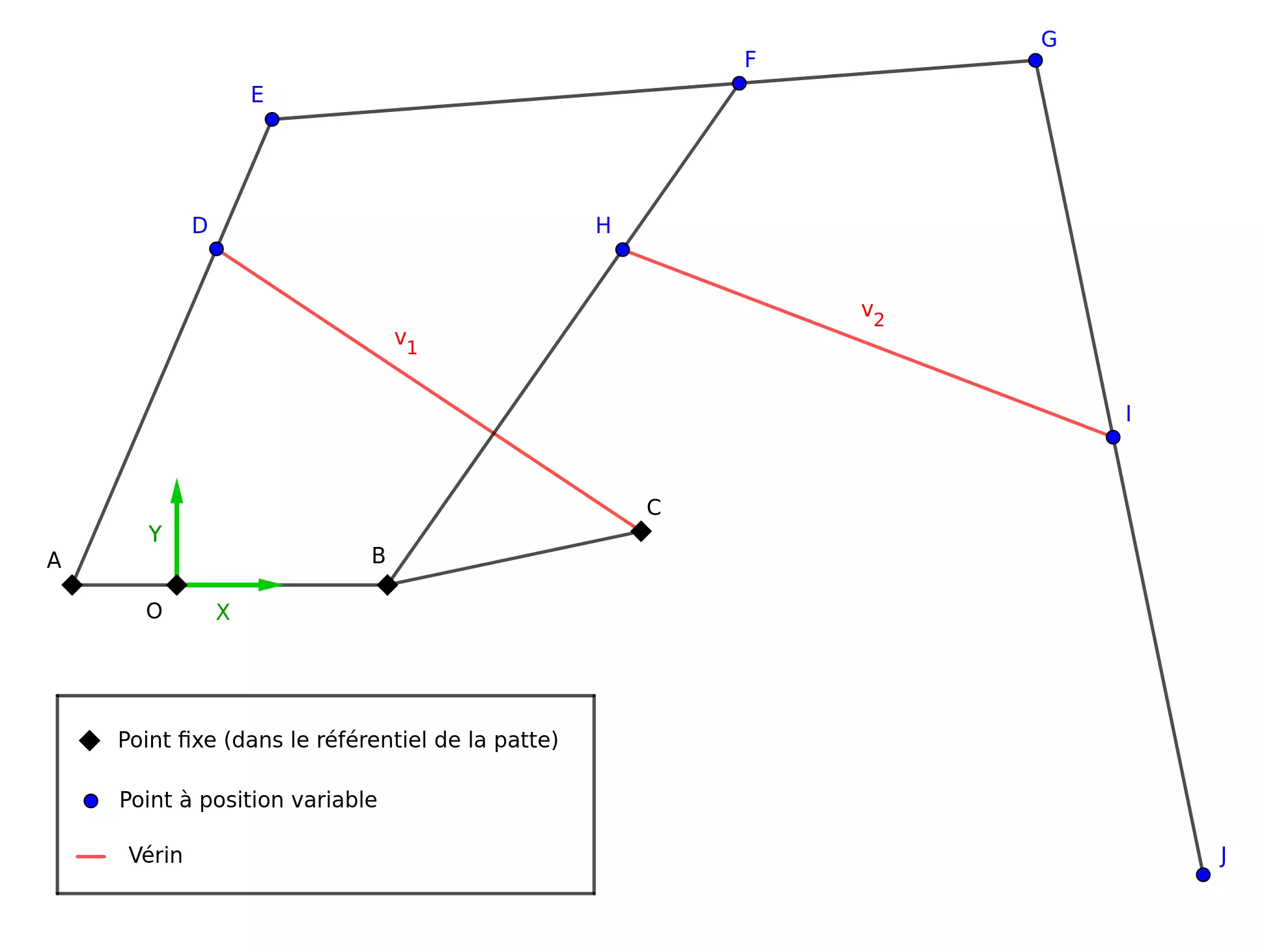
Ces calculs aboutissent à l’obtention de la matrice \(M_J\) telle que :

On remarque alors que cette matrice est la jacobienne \(J_2\) associée à notre modèle cinématique direct dans le plan de la patte :

Détails du calcul des écarts

Pour 2 points \(A\) et \(B\) d’éloignement constant, nous noterons la distance les séparant \(d_{AB}\). Le graphe des dépendances des articulations de la patte est le suivant :

 

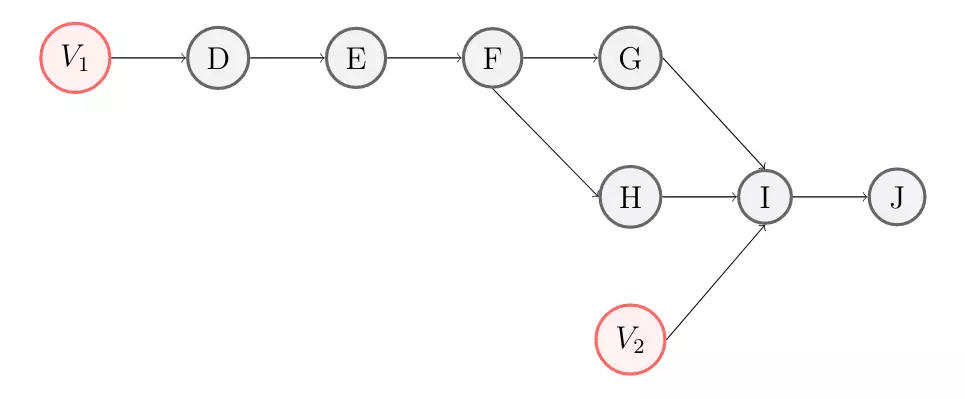
Nous cherchons tout d’abord à déterminer l’écart en \(D\). Pour cela, nous nous plaçons dans le triangle \(ADC\) où l’élongation \(v_1\) du segment \(CD\) et la position du point \(D\) sont variables. Nous obtenons le système \(S_{1}\) suivant :

\begin{equation*} S_{1} \left \{ \begin{array}{l} \left\langle \overrightarrow{AD} \middle| \overrightarrow{AD} \right\rangle - d_{AD}^{\hspace{0.1cm}2} = (x_{D} - x_{A})^{2} + (y_{D} - y_{A})^{2} - d_{AD}^{\hspace{0.1cm}2} = 0 \\ ~\\ \left\langle \overrightarrow{CD} \middle| \overrightarrow{CD} \right\rangle - v_{1}^{\hspace{0.1cm} 2} = (x_{D} - x_{C})^{2} + (y_{D} - y_{C})^{2} - v_{1}^{\hspace{0.1cm} 2} = 0 \\ \end{array} \right. \end{equation*}

 

Après dérivation par rapport à \(x_{D}\), \(y_{D}\) et \(v_1\) et à condition que \(A\), \(D\) et \(C\) ne soient pas alignés (ce qui est toujours vérifié en raison de la structure de la patte), le système \(S_{1}\) nous donne la relation matricielle suivante :

\begin{equation*} \nabla S_{1_{D, v_1}} \cdot \begin{bmatrix} \Delta x_{D}\\ \Delta y_{D}\\ \Delta v_1\\ \end{bmatrix} = \begin{bmatrix} 2(x_{D} - x_{A}) & 2(y_{D} - y_{A}) & 0 \\ 2(x_{D} - x_{C}) & 2(y_{D} - y_{C}) & -2v_{1} \end{bmatrix} \cdot \begin{bmatrix}\Delta x_{D}\\ \Delta y_{D}\\ \Delta v_1\\ \end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix} \end{equation*}

 

\begin{equation*} \Longrightarrow \hspace{0.5cm} \Delta D = \begin{bmatrix}\Delta x_{D}\\ \Delta y_{D} \end{bmatrix} = \begin{bmatrix} 2(x_{D} - x_{A}) & 2(y_{D} - y_{A}) \\ 2(x_{D} - x_{C}) & 2(y_{D} - y_{C}) \end{bmatrix}^{-1} \cdot \begin{bmatrix} 0 \\ 2v_{1} \end{bmatrix} \cdot \Delta v_{1} \end{equation*}

 

\begin{equation*} \boxed{ \Delta D = M_D \cdot \Delta v_{1} \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_D = \begin{bmatrix} 2(x_{D} - x_{A}) & 2(y_{D} - y_{A}) \\ 2(x_{D} - x_{C}) & 2(y_{D} - y_{C}) \end{bmatrix}^{-1} \cdot \begin{bmatrix} 0 \\ 2v_{1} \end{bmatrix} } \end{equation*}

 

Du fait que les points \(A\), \(D\) et \(E\) sont alignés, il est possible de déterminer l’écart de position en \(E\) à partir de l’écart de position en \(D\) en lui appliquant un simple facteur de proportionnalité.

\begin{equation*} \boxed{\Delta E = M_E \cdot \Delta v_1 \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_E = \dfrac{d_{AE}}{d_{AD}} \cdot M_D } \end{equation*}

 

Nous calculons maintenant l’écart en \(F\) en nous plaçant dans le triangle \(EBF\) où les positions de \(E\) et \(F\) sont variables. Nous obtenons le système \(S_2\) suivant :

\begin{equation*} S_{2} \left \{ \begin{array}{l} \left\langle \overrightarrow{EF} \middle| \overrightarrow{EF} \right\rangle - d_{EF}^{\hspace{0.1cm}2} = (x_{F} - x_{E})^{2} + (y_{F} - y_{E})^{2} - d_{EF}^{\hspace{0.1cm}2} = 0 \\ ~\\ \left\langle \overrightarrow{BF} \middle| \overrightarrow{BF} \right\rangle - d_{BF}^{\hspace{0.1cm}2} = (x_{F} - x_{B})^{2} + (y_{F} - y_{B})^{2} - d_{BF}^{\hspace{0.1cm}2} = 0 \\ \end{array} \right. \end{equation*}

 

Nous le dérivons par rapport à \(x_{F}\), \(y_{F}\), \(x_{E}\) et \(y_{E}\), et à condition que \(B\), \(E\) et \(F\) ne soient pas alignés (ce qui est toujours vérifié en raison de la structure de la patte), nous obtenons :

\begin{equation*} \nabla S_{2_{F, E}} \cdot \begin{bmatrix} \Delta x_{F} \\ \Delta y_{F} \\ \Delta x_{E} \\ \Delta y_{E} \end{bmatrix} = \begin{bmatrix} 2(x_{F} - x_{E}) & 2(y_{F} - y_{E}) & -2(x_{F} - x_{E}) & -2(y_{F} - y_{E}) \\ 2(x_{F} - x_{B}) & 2(y_{F} - y_{B}) & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} \Delta x_{F} \\ \Delta y_{F} \\ \Delta x_{E} \\ \Delta y_{E} \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ \end{bmatrix} \end{equation*}

 

\begin{equation*} \Longrightarrow \hspace{0.5cm} \Delta F = \begin{bmatrix} \Delta x_{F}\\ \Delta y_{F} \end{bmatrix} = \begin{bmatrix} 2(x_{F} - x_{E}) & 2(y_{F} - y_{E}) \\ 2(x_{F} - x_{B}) & 2(y_{F} - y_{B}) \\ \end{bmatrix}^{-1} \cdot \begin{bmatrix} 2(x_{F} - x_{E}) & 2(y_{F} - y_{E}) \\ 0 & 0 \end{bmatrix} \cdot \Delta E \end{equation*}

 

\begin{equation*} \boxed{\Delta F = M_F \cdot \Delta v_1 \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_F = \begin{bmatrix} 2(x_{F} - x_{E}) & 2(y_{F} - y_{E}) \\ 2(x_{F} - x_{B}) & 2(y_{F} - y_{B}) \\ \end{bmatrix}^{-1} \cdot \begin{bmatrix} 2(x_{F} - x_{E}) & 2(y_{F} - y_{E}) \\ 0 & 0 \end{bmatrix} \cdot M_E} \end{equation*}

 

Les points \(E\), \(F\) et \(G\) d’une part et \(B\), \(F\) et \(H\) d’autre part sont alignés. On peut donc obtenir les écarts en \(G\) et en \(H\) à partir de l’écart en \(F\) :

\begin{equation*} \boxed{\Delta G = M_{G} \cdot \Delta v_{1} \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_G = \dfrac{d_{EG}}{d_{EF}} \cdot M_F} \end{equation*}

 

\begin{equation*} \boxed{\Delta H = M_{H} \cdot \Delta v_{1} \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_H = \dfrac{d_{BH}}{d_{BF}} \cdot M_F} \end{equation*}

 

Nous pouvons à présent obtenir l’écart en \(I\) en nous plaçant dans le triangle \(GHI\) où les positions des points \(G\) et \(H\) ainsi que l’élongation \(v_2\) du segment \(HI\) sont variables. Nous obtenons le système \(S_3\) suivant :

\begin{equation*} S_{3} \left \{ \begin{array}{l} \left\langle \overrightarrow{GI} \middle| \overrightarrow{GI} \right\rangle - d_{GI}^{\hspace{0.1cm}2} = (x_{I} - x_{G})^{2} + (y_{I} - y_{G})^{2} - d_{GI}^{\hspace{0.1cm}2} = 0 \\ ~\\ \left\langle \overrightarrow{HI} \middle| \overrightarrow{HI} \right\rangle - v_{2}^{\hspace{0.1cm} 2} = (x_{I} - x_{H})^{2} + (y_{I} - y_{H})^{2} - v_{2}^{\hspace{0.1cm} 2} = 0 \\ \end{array} \right. \end{equation*}

 

Nous le dérivons par rapport à \(x_{I}\), \(y_{I}\), \(x_{G}\), \(y_{G}\), \(x_{H}\), \(y_{H}\) et \(v_{2}\) pour obtenir la jacobienne suivante :

\begin{equation*} \nabla S_{3_{I, G, H, v_{2}}} = \begin{bmatrix} M_{1} & -M_{2} & -M_{3} & -M_{4} \end{bmatrix} \hspace{0.2cm} \text{avec} \end{equation*}

 

\begin{equation*} M_1 = \begin{bmatrix} 2(x_{I} - x_{G}) & 2(y_{I} - y_{G}) \\ 2(x_{I} - x_{H}) & 2(y_{I} - y_{H}) \end{bmatrix} \hspace{2cm} M_2 = \begin{bmatrix} 2(x_{I} - x_{G}) & 2(y_{I} - y_{G}) \\ 0 & 0 \end{bmatrix} \end{equation*}

 

\begin{equation*} \hspace{-3.55cm} M_3 = \begin{bmatrix} 0 & 0 \\ 2(x_{I} - x_{H}) & 2(y_{I} - y_{H}) \end{bmatrix} \hspace{2cm} M_4 = \begin{bmatrix} 0 \\ 2 v_2 \end{bmatrix} \end{equation*}

 

On a alors la relation suivante permettant de relier l’écart en \(I\) à \(\Delta v_1\) et \(\Delta v_2\) à la condition que \(I\), \(G\) et \(H\) ne soient pas alignés (ce qui est toujours vérifié en raison de la structure de la patte) :

\begin{equation*} \Delta I = M_{1}^{-1} \cdot \left( M_{2} \cdot \Delta G + M_{3} \cdot \Delta H + M_{4} \cdot \Delta v_{2} \right) = M_{1}^{-1} \cdot \left( M_{2} \cdot M_{G} + M_{3} \cdot M_{H} \right) \cdot \Delta v1 + M_{1}^{-1} \cdot M_{4} \cdot \Delta v_{2} \end{equation*}

 

\begin{equation*} \boxed{ \array{ \Delta I = M_I \cdot \begin{bmatrix} \Delta v_{1}\\ \Delta v_{2} \end{bmatrix} \\[0.2cm] \text{avec} \\[0.2cm] \hspace{0.2cm} M_I = \begin{bmatrix} V1 & V2 \end{bmatrix} \hspace{1cm} V_1 = M_{1}^{-1} \cdot \left( M_{2} \cdot M_{G} + M_{3} \cdot M_{H} \right) \hspace{1cm} V_2 = M_{1}^{-1} \cdot M_{4} \hspace{0.2cm}}} \end{equation*}

 

Enfin, du fait que \(G\), \(I\) et \(J\) sont alignés, on obtient l’écart de position en \(J\) :

\begin{equation*} \boxed{\Delta J = M_J \cdot \begin{bmatrix} \Delta v_{1}\\ \Delta v_{2} \end{bmatrix} \hspace{0.2cm} \text{avec} \hspace{0.2cm} M_J = \dfrac{d_{GJ}}{d_{GI}} \cdot M_I} \end{equation*}

 

Cinématique directe dans l’espace de la patte

L’objectif à présent est de ramener notre modèle dans l’espace en ajoutant l’influence du vérin \(v_3\) sur notre cinématique directe. Le référentiel cible est le référentiel \((\overrightarrow{x}, \overrightarrow{y}, \overrightarrow{z})\) représenté sur la figure suivante. On notera que le vecteur \(\overrightarrow{Y}\) utilisés dans la partie précédente est devenu le vecteur \(\overrightarrow{Z}\) dans cette modélisation à des fins de convention.

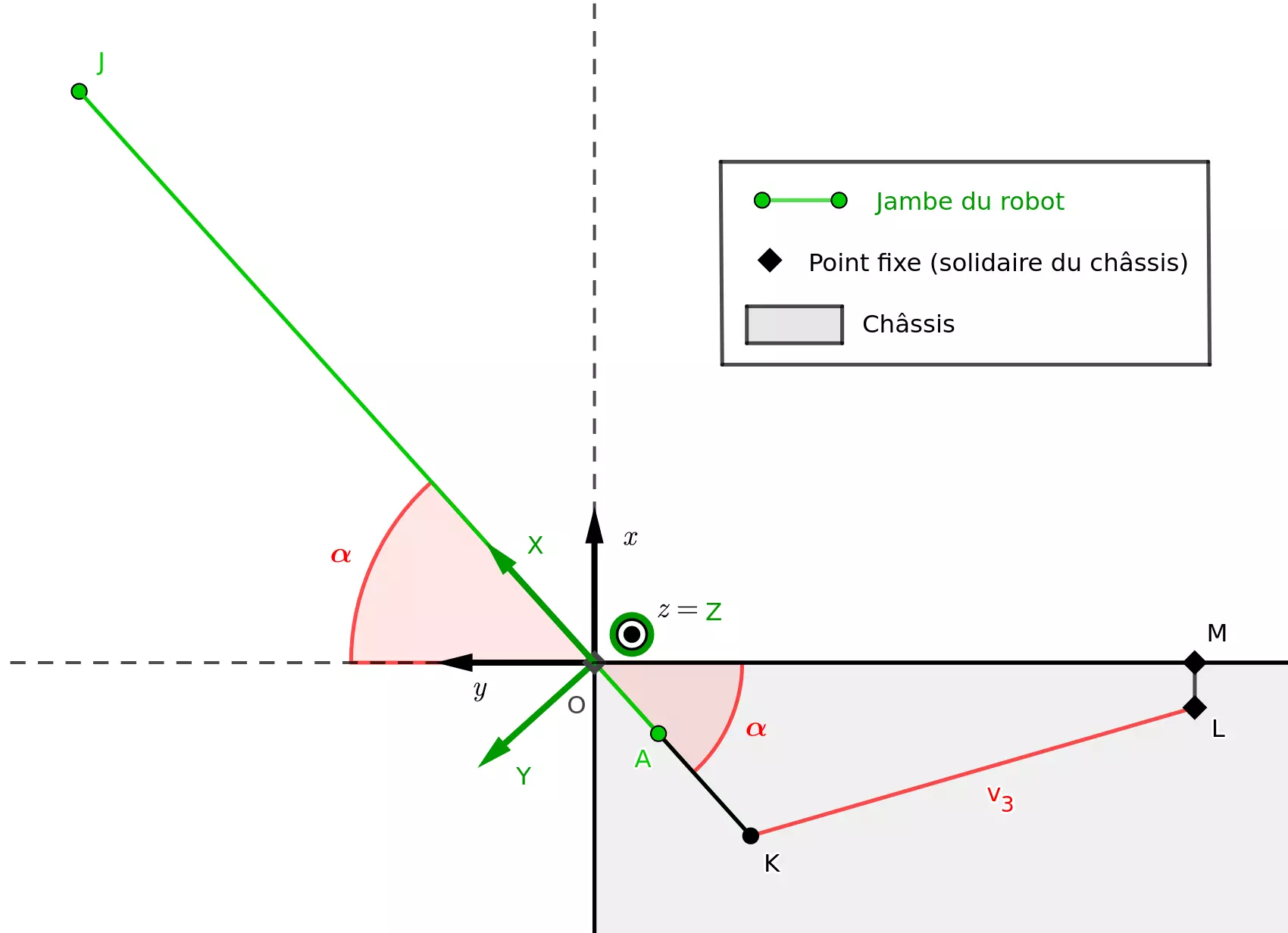
Soit \((X, Z)\) les coordonnées de l’extrémité \(J\) de la patte dans son plan. Il faut tout d’abord exprimer l’angle \(\alpha\) de la patte au châssis en fonction de l’élongation du vérin \(v_3\). Cela permet d’aboutir à une expression des variations de \(X\), \(Z\) et \(\alpha\) en fonction des variations de \(v_1\), \(v_2\) et \(v_3\).

Une fois cette relation explicitée, il faut traduire la rotation d’angle \(\alpha\) autour de l’axe \(\overrightarrow Z\) sous forme matricielle afin de se ramener au référentiel \((\overrightarrow x, \overrightarrow y, \overrightarrow z)\). On obtient alors la relation suivante :

A partir des matrices \(A\) et \(B\), il devient possible de construire \(J_3\), la matrice reliant \((\Delta x, \Delta y, \Delta z)\) à \((\Delta v_1, \Delta v_2, \Delta v_3)\) :

Détails du changement de référentiel

En premier lieu, nous cherchons à exprimer l’angle \(\alpha\) de la patte au châssis en fonction de l’élongation du vérin \(v_3\). Pour cela, nous nous plaçons dans le triangle \(KLO\).

 

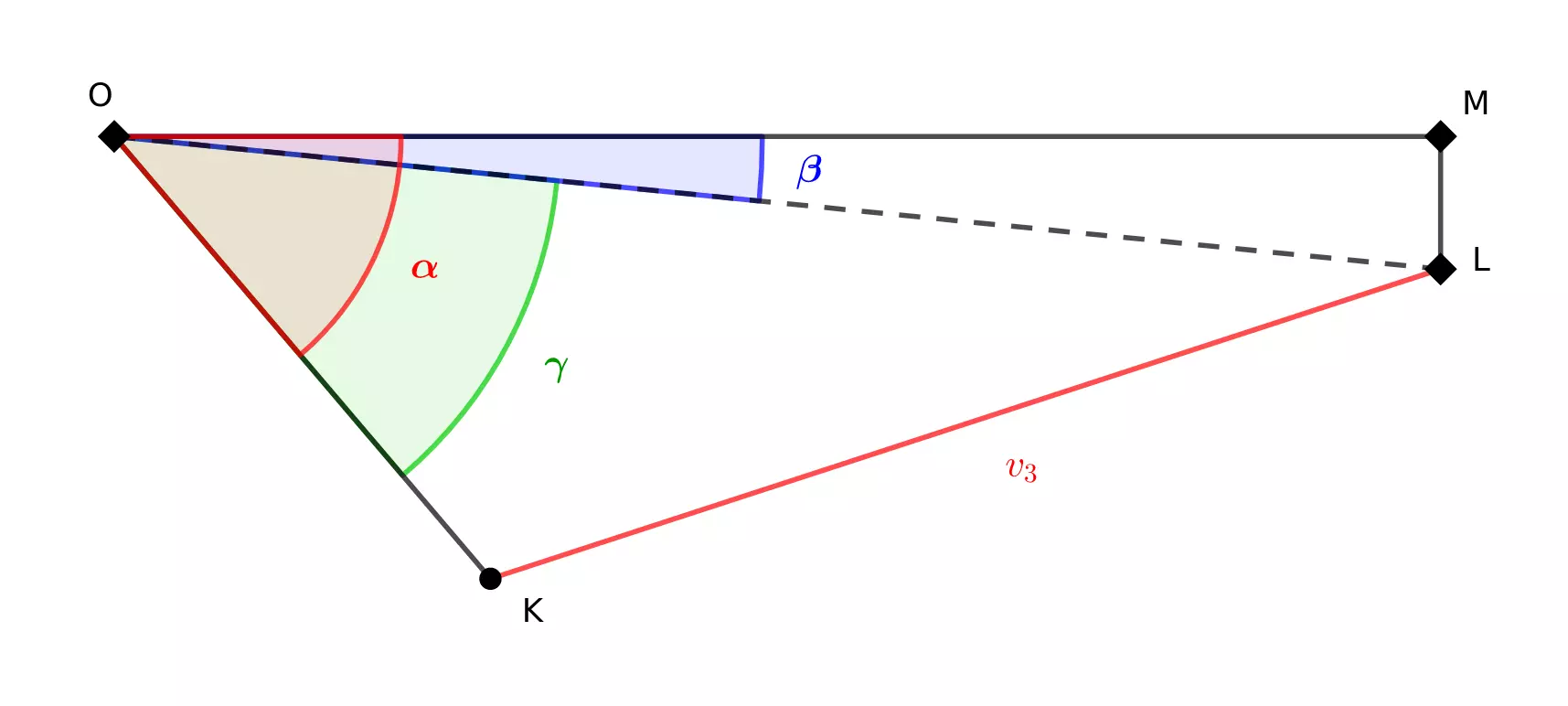
En utilisant la loi des cosinus, nous obtenons la relation suivante :

\begin{equation*} \begin{array}{lc} &d_{OK} \cdot d_{OL} \cdot \cos{\gamma} = \dfrac{1}{2} ( d_{OK}^{\hspace{0.1cm} 2} + d_{OL}^{\hspace{0.1cm} 2} - v_3^{\hspace{0.1cm} 2}) \\~\\ \implies & \dfrac{d_{OK}}{d_{OL}} + \dfrac{d_{OL}}{d_{OK}} - \dfrac{v_3}{d_{OK} d_{OL}} - 2 \cdot \cos(\gamma) = 0 \end{array} \end{equation*}

 

Nous construisons ensuite la jacobienne associée, ce qui nous permet d’obtenir la relation matricielle suivante :

\begin{equation*} \begin{bmatrix} 2 \cdot \sin(\gamma) & \dfrac{- 2 \cdot v_3}{d_{OK}d_{OL}} \end{bmatrix} \cdot \begin{bmatrix} \Delta \gamma \\ \Delta v_3 \end{bmatrix} = 0 \end{equation*}

 

Du fait que \(\Delta \alpha\) soit égal à \(\Delta \gamma\), nous obtenons enfin la relation suivante :

\begin{equation*} \boxed{ \Delta \alpha = \dfrac{v_3}{\sin{(\alpha - \beta)} \cdot d_{OK} d_{OL}} \cdot \Delta v_3 } \end{equation*}

 

L’obtention de la relation entre \(\Delta \alpha\) et \(\Delta v_3\) nous permet d’obtenir la matrice liant \(( \Delta X, \Delta Z, \Delta\alpha )\) à \((\Delta v_1, \Delta v_2, \Delta v_3)\). Pour cela, nous réutilisons \(J_2\) obtenue lors de la résolution de la cinématique directe dans le plan de la patte :

\begin{equation*} \boxed{ \begin{bmatrix} \Delta X \\ \Delta Z \\ \Delta\alpha \end{bmatrix} = A \cdot \begin{bmatrix} \Delta v_{1} \\ \Delta v_{2} \\ \Delta v_{3} \end{bmatrix} \hspace{0.2cm} \text{avec} \hspace{0.2cm} A = \begin{bmatrix} J_2 & \begin{matrix}0 \\ 0\end{matrix} \\ \begin{matrix} 0 & 0\end{matrix} & \dfrac{v_3}{\sin(\alpha - \beta) \cdot d_{OK}d_{OL}} \end{bmatrix}} \end{equation*}

 

La seconde étape permettant l’obtention de notre jacobienne dans le référentiel \((\overrightarrow{x}, \overrightarrow{y}, \overrightarrow{z})\) est d’obtenir la matrice reliant \((\Delta x, \Delta y, \Delta z)\) à \((\Delta X, \Delta Z, \Delta \alpha)\). Pour cela, nous devons étudier la rotation d’angle \(\alpha\) séparant \((\overrightarrow{X}, \overrightarrow{Y}, \overrightarrow{Z})\) et \((\overrightarrow{x}, \overrightarrow{y}, \overrightarrow{z})\).

 

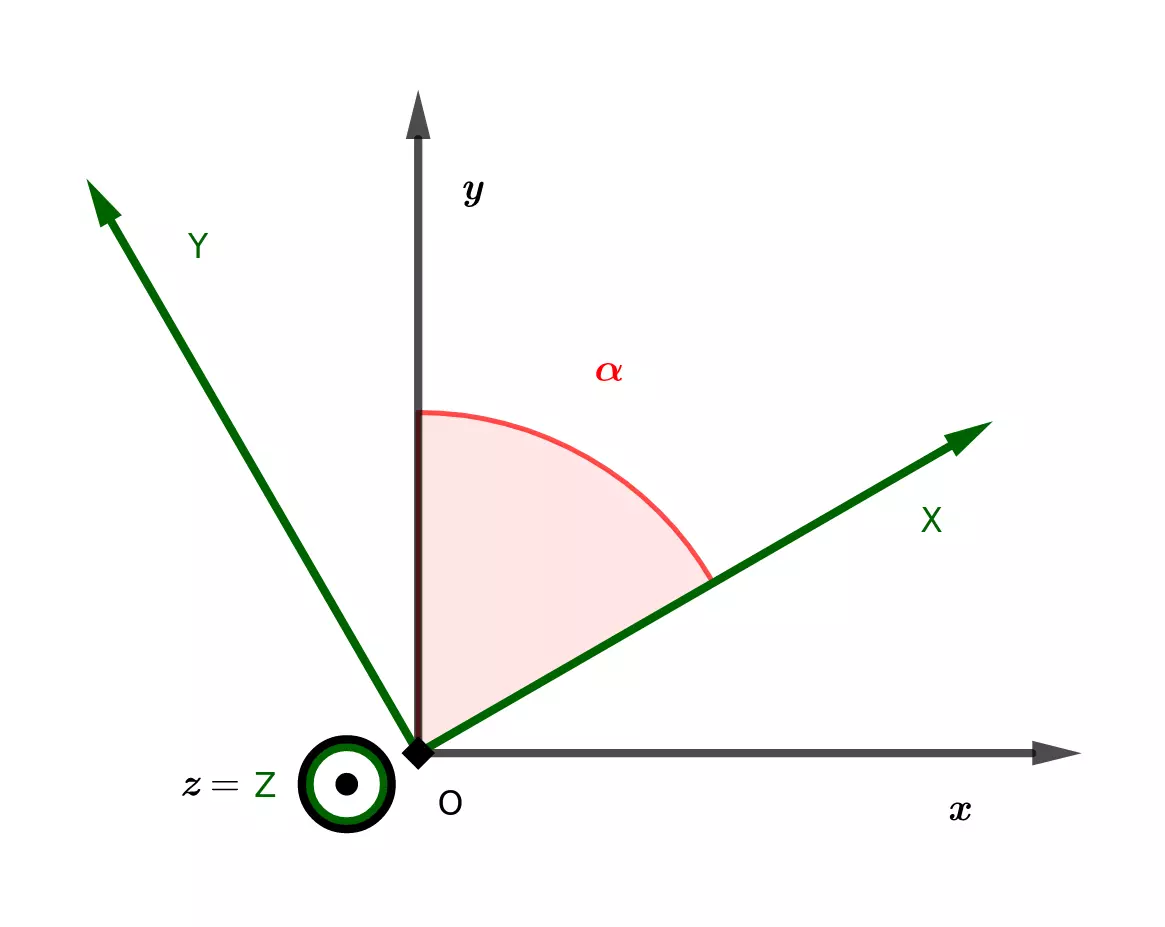
Nous notons tout d’abord que l’inégalité \(0<\alpha<\dfrac{\pi}{2}\) est toujours vérifiée de par la structure du châssis. De ce fait, nous nous autorisons l’expression de la rotation d’un angle de \(\dfrac{\pi}{2} - \alpha\) sans nous questionner sur le signe de l’angle de rotation.

\begin{equation*} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = R_{\frac{\pi}{2} - \alpha} \cdot \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \hspace{0.2cm} \text{avec} \hspace{0.2cm} R_{\frac{\pi}{2} - \alpha} = \begin{bmatrix} \cos(\frac{\pi}{2}-\alpha) & -\sin(\frac{\pi}{2}-\alpha) & 0\\ \sin(\frac{\pi}{2}-\alpha) & \cos(\frac{\pi}{2}-\alpha) & 0\\ 0& 0& 1 \end{bmatrix} \end{equation*}

 

En dérivant cette relation par rapport à \(\alpha\), nous obtenons la relation suivante :

\begin{equation*} \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} = \dfrac{\partial R_{\frac{\pi}{2} - \alpha}}{\partial\alpha} \cdot \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \cdot \Delta \alpha + R_{\frac{\pi}{2} - \alpha} \cdot \begin{bmatrix} \Delta X \\ \Delta Y \\ \Delta Z \end{bmatrix} \end{equation*}

 

\begin{equation*} \text{où} \hspace{0.5cm} \dfrac{\partial R_{\frac{\pi}{2} - \alpha}}{\partial\alpha} = \begin{bmatrix} \sin(\frac{\pi}{2}-\alpha) & \cos(\frac{\pi}{2}-\alpha) & 0\\ -\cos(\frac{\pi}{2}-\alpha) & \sin(\frac{\pi}{2}-\alpha) & 0\\ 0& 0& 0 \end{bmatrix} \end{equation*}

 

Nous savons que \(Y\) et \(\Delta Y\) sont constant dans notre modèle et valent \(Y = 0\) et \(\Delta Y = 0\). De ce fait il nous est possible de simplifier la relation précédente en :

\begin{equation*} \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} = \begin{bmatrix} X \cdot \sin(\frac{\pi}{2}-\alpha) \\ -X \cdot \cos(\frac{\pi}{2}-\alpha) \\ 0 \end{bmatrix} \cdot \Delta \alpha + \begin{bmatrix} \cos(\frac{\pi}{2}-\alpha) & 0\\ \sin(\frac{\pi}{2}-\alpha) & 0\\ 0& 1 \end{bmatrix} \begin{bmatrix} \Delta X \\ \Delta Z \end{bmatrix} \end{equation*}

 

Ou bien, formulé autrement :

\begin{equation*} \boxed{ \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} = B \cdot \begin{bmatrix} \Delta X \\ \Delta Z \\ \Delta \alpha \end{bmatrix} \hspace{0.2cm} \text{avec} \hspace{0.2cm} B = \begin{bmatrix} \cos(\frac{\pi}{2}-\alpha) & 0 & X \cdot \sin(\frac{\pi}{2}-\alpha) \\ \sin(\frac{\pi}{2}-\alpha) & 0 & -X \cdot \cos(\frac{\pi}{2}-\alpha)\\ 0 & 1 & 0 \end{bmatrix}} \end{equation*}

 

Généralisation

Nous avons explicité \(J_3\), la jacobienne associée au modèle cinématique direct d’une patte du Megabot dans son référentiel. Afin de pouvoir appliquer un contrôle simultané sur l’ensemble des pattes, il est nécessaire de généraliser notre modèle cinématique à l’ensemble de notre robot.

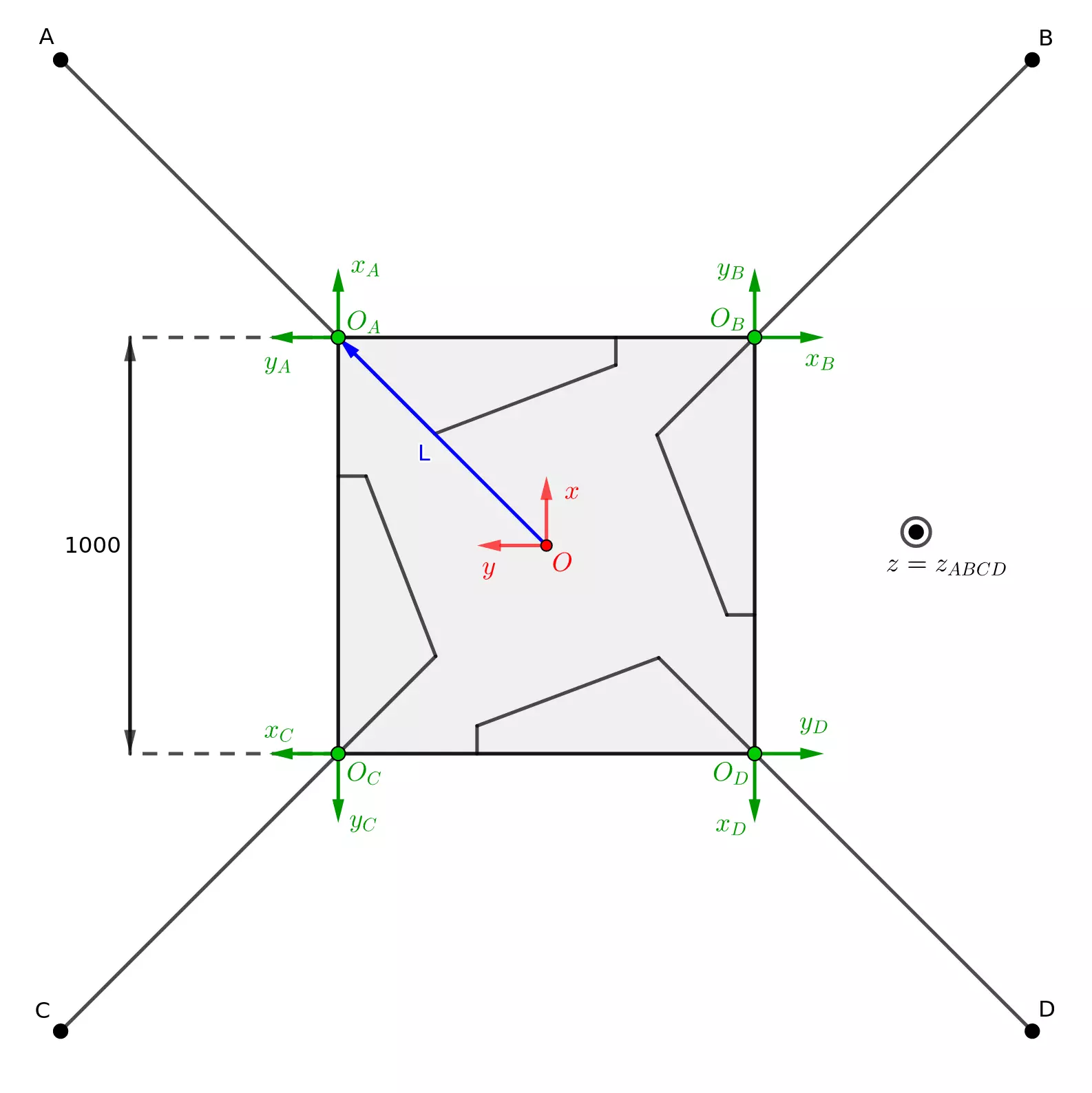
Nous noterons à partir de maintenant \(\Delta V\) les variations d’élongation des 12 vérins et \(\Delta X\) les variations de position de l’extrémité des pattes dans le référentiel \((\overrightarrow{x}, \overrightarrow{y}, \overrightarrow{z})\) du robot. La nouvelle matrice de passage entre ces vecteurs sera nommée \(J_{12}\) :

On peut alors remarquer qu’en utilisant des matrices de rotation il est facile d’exprimer \(J_{12}\) à partir de \(J_3\) qui a été calculée dans la partie précédente :

Les jacobiennes \(J_2\), \(J_3\) et \(J_{12}\) calculées permettent toutes d’élaborer des algorithmes de contrôle respectivement d’une patte dans son plan, d’une patte dans son référentiel et de l’ensemble des pattes dans le référentiel du Megabot en utilisant un solveur QP. Néanmoins, la problématique importante de gestion du centre de gravité peut également être traitée dès la phase de contrôle, c’est pourquoi nous allons l’intégrer à nos équations.

Gestion du centre de gravité

En effet, une problématique importante que nous allons chercher à résoudre est le maintien du projeté du centre de gravité du robot dans son polygone de sustentation, c’est à dire le polygone convexe formé par les points de contact entre le sol et le robot. Dans le cas où le centre de gravité du Megabot viendrait à ne plus être au dessus de cette zone alors il basculerait, ce qui modifierait ses pattes au sol et fausserait toute planification de mouvement.

Nous avons implémenté 2 modes de contrôle principaux, chacun ayant des avantages et inconvénients. Le premier ne fait que contraindre le centre de gravité au dessus du polygone de sustentation par l’ajout de contraintes dans le solveur QP. Le second quant à lui permet de fournir en entrée non pas seulement une trajectoire pour les pattes du robot, mais également pour son centre de gravité.

Dans les 2 cas, il est nécessaire d’élaborer la jacobienne associée au déplacement du centre de gravité du Megabot. Connaissant le poids de chacune des pièces du Megabot, il est possible de déterminer les variations \(\Delta C\) du centre de gravité à partir de \(\Delta V\) et des jacobiennes du modèle cinématique direct. En effet la position du centre de gravité n’est qu’une combinaison linéaire des positions de chacune des articulations du robot. On obtient alord une relation du type :

Contrainte du centre de gravité

Une fois la jacobienne \(J_C\) explicitée, il devient possible d’utiliser les variables \(G\) et \(h\) du solveur QP afin de contraindre le centre de gravité. En posant \(G = J_C\) et en choisissant \(h\) en accord avec les contraintes à appliquer au centre de gravité, le solveur garantira alors :

Notons qu’ici chaques lignes de \(G\) et \(h\) correspondent à une contrainte sur une coordonnées de centre de gravité. Dans les faits, on souhaite contraindre le projeté du centre de gravité dans le polygone de sustentation, il faut donc construire \(G\) de sorte à ce que chacune de ses lignes soit une combinaison linéaire des lignes de \(J_{C}\), tandis que \(h\) contiendrait les valeurs de contrainte associées. Dans le cas où nous aurions besoin de \(n\) contraintes sur les coordonnées du centre de gravité pour le maintenir dans les polygone de sustentation, \(G\) et \(h\) seraient alors constitués de \(n\) lignes.

Cette solution apporte une forme de sécurité tout en laissant au centre de gravité une certaine liberté. Elle semble adaptée à un robot possédant une zone de sustentation constante au cours de son déplacement car, le cas échéant, elle permet de contraindre le centre de gravité à cette zone et de ne plus avoir à s’en préoccuper durant la phase de planification.

Ce n’est malheureusement pas le cas du Megabot, c’est pourquoi nous avons opté pour la seconde solution qui offre un contrôle exact du centre de gravité mais qui en contrepartie nécessite sa prise en compte dans la planification.

Contrôle du centre de gravité

Afin de commander la position du centre de gravité, il est nécessaire de l’intégrer aux entrées du solveur QP. On obtient alors la relation suivante en reprenant les notations précédentes:

La nouvelle jacobienne \(J_{15:12}\) ainsi construite permet bien de prendre en compte la position du centre de gravité dans notre cinématique directe, néanmoins la matrice \(J_{15:12}\) ne peut pas être exploitée telle quelle par le solveur QP car la matrice \(J_{15:12}\hspace{0.15cm}^TJ_{15:12}\) est singulière (cf. démonstration effectuée en début de partie). Une solution pour contourner la singularité de cette matrice, est d’ajouter un terme de régularisation à notre minimisation.

Détails de l'ajout d'un terme de régularisation

Planification

La phase de planification consiste en l’élaboration du mouvement indépendemment des réflexions liées au contrôle. Il s’agit de savoir ce que va faire le robot et non comment il va le réaliser et se traduit par l’implémentation d’algorithmes fournissant des positions successives pour les pattes et le centre de gravité du Megabot.

Elaboration des trajectoires

Nous avions pour objectif de permettre au Megabot un déplacement courbe. De ce fait nous avons tout d’abord cherché à traduire une entrée de direction (2 dimensions) et de rotation (1 dimension) en une trajectoire pour le Megabot. Cette modélisation a pour objectif de pouvoir commander le robot à l’aide d’une manette à 2 joysticks.

La direction permet de définir le vecteur \(\overrightarrow{d}\) représenté sur le schéma suivant tandis que la valeur de rotation permet de définir la position du centre de rotation \(R\) sur l’axe perpendiculaire à la direction : plus la valeur est proche de 0, moins la courbe est importante et plus \(R\) est éloigné, à droite pour une rotation positive et à gauche pour une rotation négative. Les trajectoires des 4 pattes sont ensuite déterminées en traçant les cercles de centre \(R\) passant par leurs extrémités.

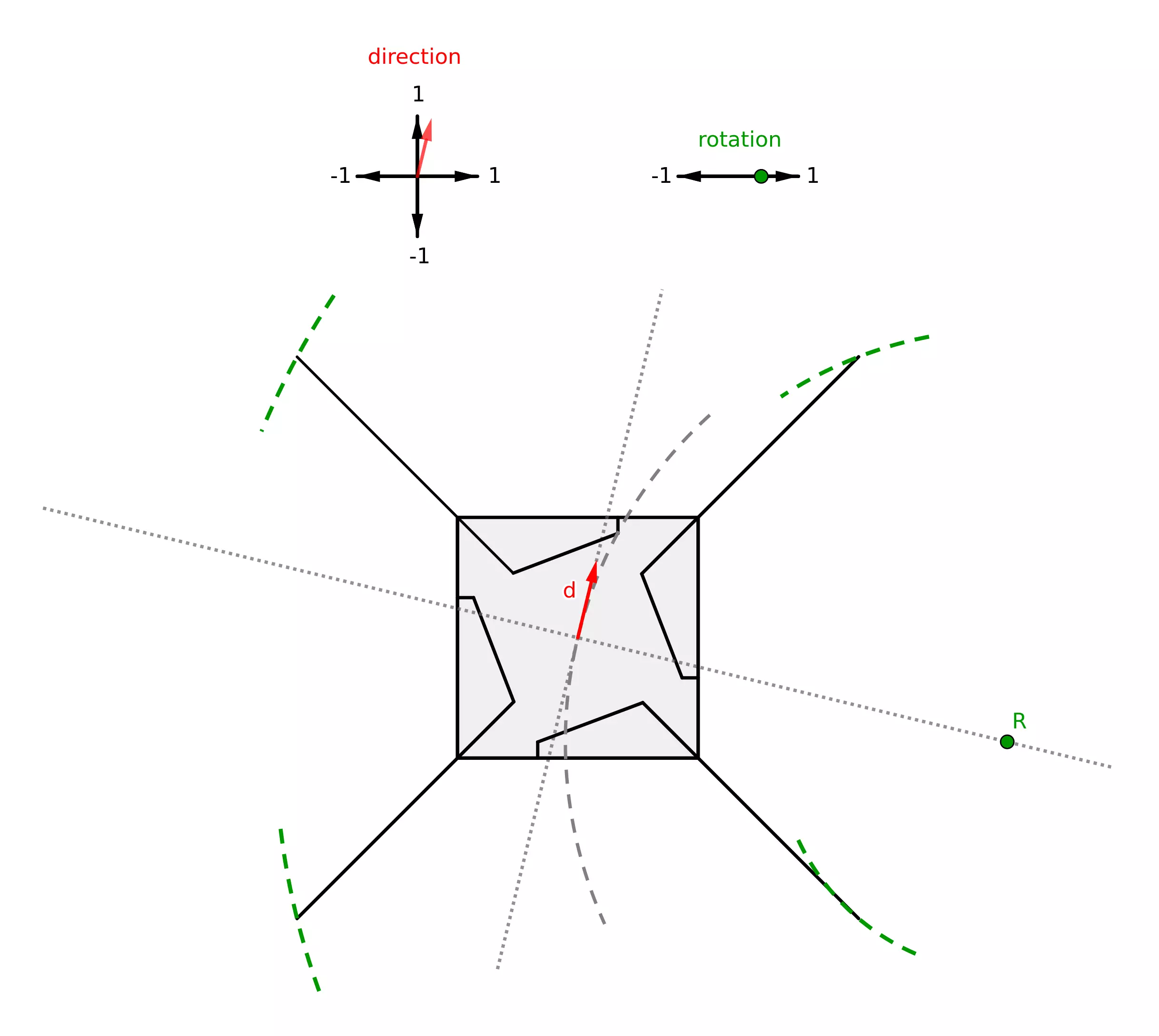
Dans le cas d’une direction nulle et d’une rotation, \(R\) est placé au centre du Megabot. Dans le cas d’une rotation nulle et d’une direction, les trajectoires des pattes sont simplement des droites parallèles à l’axe de direction.

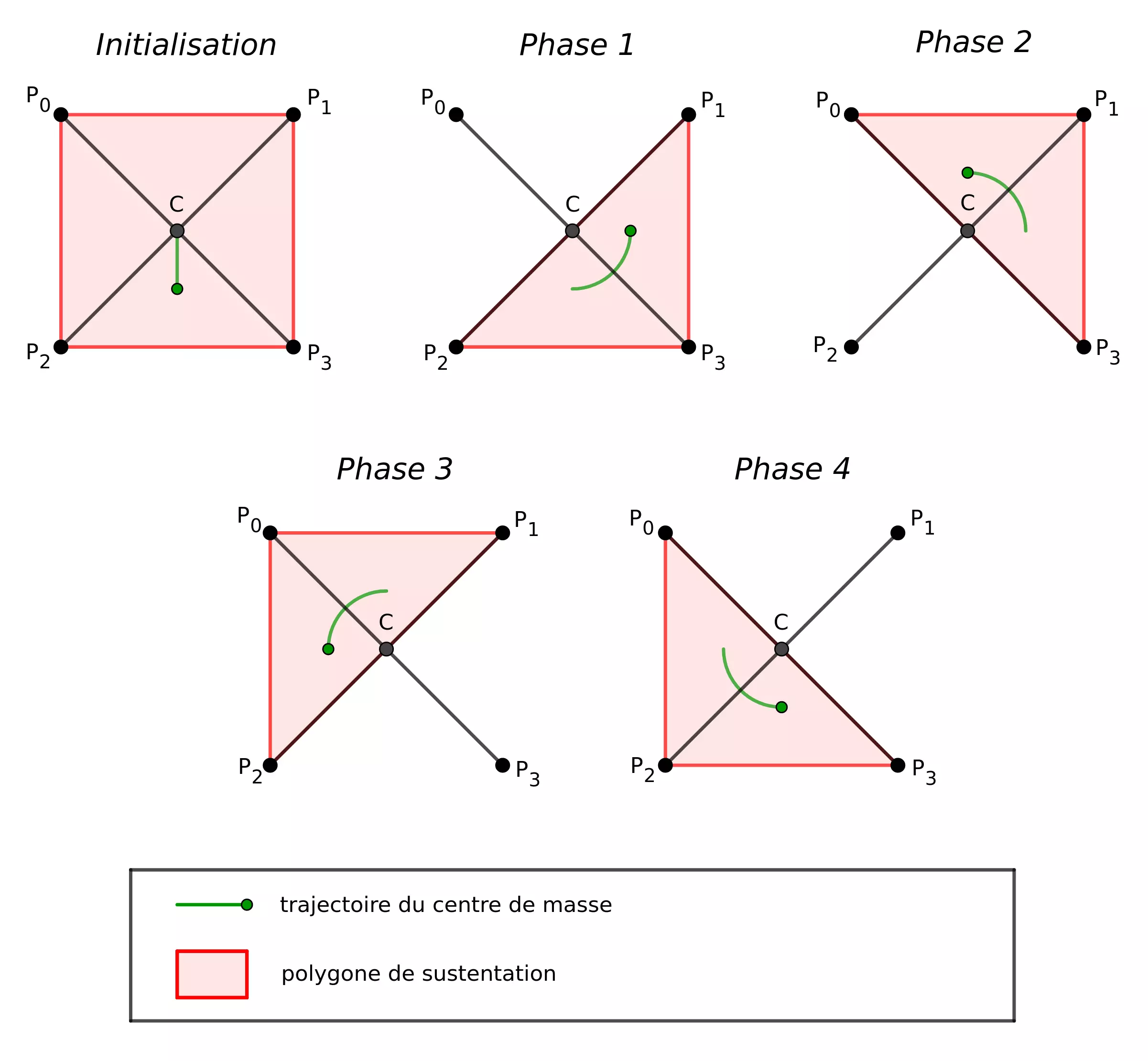
Une fois les trajectoires des 4 pattes déterminées, nous nous sommes questionnés sur la gestion du centre de gravité du robot. La solution retenue permettant de garantir que le centre de gravité soit constamment au dessus du triangle de sustentation a été de lui faire suivre une trajectoire circulaire autour de l’intersection des diagonales du polygone formé par les extrémités des 4 pattes \(P_0\), \(P_1\), \(P_2\) et \(P_3\) durant leur déplacement. Nous noterons ce point \(C\) dans la suite des explications. Ce choix nous amène à un découpage de notre marche en 4 phases, précédées d’une phase d’initialisation :

Algorithme de marche

Une fois les trajectoires des extrémités des 4 pattes et du centre de gravité établies, nous avons pour chacune des phases détaillées sur la figure précédente procédé à une discrétisation du parcours des pattes et du centre de gravité. Le point \(C\) est mis à jour à chaque étape de cette discrétisation, ce qui assure un maintien du centre de gravité au dessus du polygone de sustentation.

Durant la phase d’initialisation, les 4 pattes sont fixes au sol et le centre de gravité est déplacé vers l’arrière du Megabot. Ensuite, lors de chacune des phases suivantes, une patte est levée, déplacée le long de sa trajectoire puis abaissée en même temps que le centre de gravité effectue un quart de tour autour de \(C\). Cette stratégie implique que les pattes sont déplacées une à une dans le sens anti-horaire. L’algorithme de contrôle implémenté dans la partie Contôle permet de traduire cette commande en élongations de vérins et d’effectuer la marche.

Simulation

Afin de vérifier notre algorithme de marche il est nécessaire de procéder à une simulation du Megabot. En effet, bien que nous ayons effectué des tests unitaires et d’intégration de nos fonctions au cours du développement, tester directement notre marche sur le Megabot réel serait trop précipité, car dans le cas où nous constaterions des écarts entre le résultat et le comportement attendu, rien ne nous garantirait que l’erreur proviendrait bien de notre partie algorithmique et non de notre électronique ou de notre mécanique.

Afin de simuler la physique lors des tests de marche du Megabot, nous avons choisis d’utiliser PyBullet. Ce choix implique tout d’abord la réalisation d’un fichier URDF contenant une modélisation du Megabot.

Le format URDF représente les robots sous forme d’un arbre de pièces reliées par des liaisons (pivot, glissière, etc). Cette modélisation très commune est adaptée actionné par des moteurs aux articulations, mais empêche la formation de cycle et donc toute fermeture géométrique au sein de la structure du robot. Comme l’ensemble des mouvements du Megabot repose sur des boucles cinématiques au niveau des vérins, il a été nécessaire de trouver un moyen de contourner ce problème. La solution trouvée a été de réaliser un modèle cinématique incomplet et de rajouter des contraintes refermant les boucles a posteriori dans PyBullet.

Une première étape a été la modélisation du Megabot sur OnShape, en incluant le maximum de détail possible et en renseignant le poids et les matrices inertielles de chaque pièce. L’ensemble des liaisons entre les pièces ont été construites dans un assemblage, excepté pour celles amenant des fermetures géométriques, puis le modèle OnShape a été converti en URDF en utilisant l’outil \(\verb|onshape-to-robot|\).

Une fois l’URDF généré, les contraintes de fermetures géométriques ont été construites via PyBullet, et la simulation de la marche a pu être réalisée.